1. Goal
The goal is to perform Data-free Knowledge distillation.
Knowledge distillation: Dealing with the problem of training a smaller model (Student) from a high capacity source model (Teacher) so as to retain most of its performance.
As the word itself, We perform knowledge distillation when there is no original dataset on which the Teacher network has been trained. It is because, in the real world, most datasets are proprietary and not shared publicly due to privacy or confidentiality concerns.
To tackle this problem, it is necessary to reconstruct a dataset for training Student network. Thus, in Dreaming to Distill Data-free Knowledge Transfer via DeepInversion, we propose a new method, which synthesizes images from the image distribution used to train a deep neural network. Further, we aim to improve the diversity of synthesized images.
2. Method
- Proposing DeepInversion, a new method for synthesizing class-conditional images from a CNN trained for image classification.
- Introducing a regularization term for intermediate layer activations of synthesized images based on just the two layer-wise statistics: mean and variance from teacher network.
- Improving synthesis diversity via application-specific extension of DeepInversion, called Adaptive DeepInversion.
- Exploiting disagreements between the pretrained teacher and the in-training student network to expand the coverage of the training set.
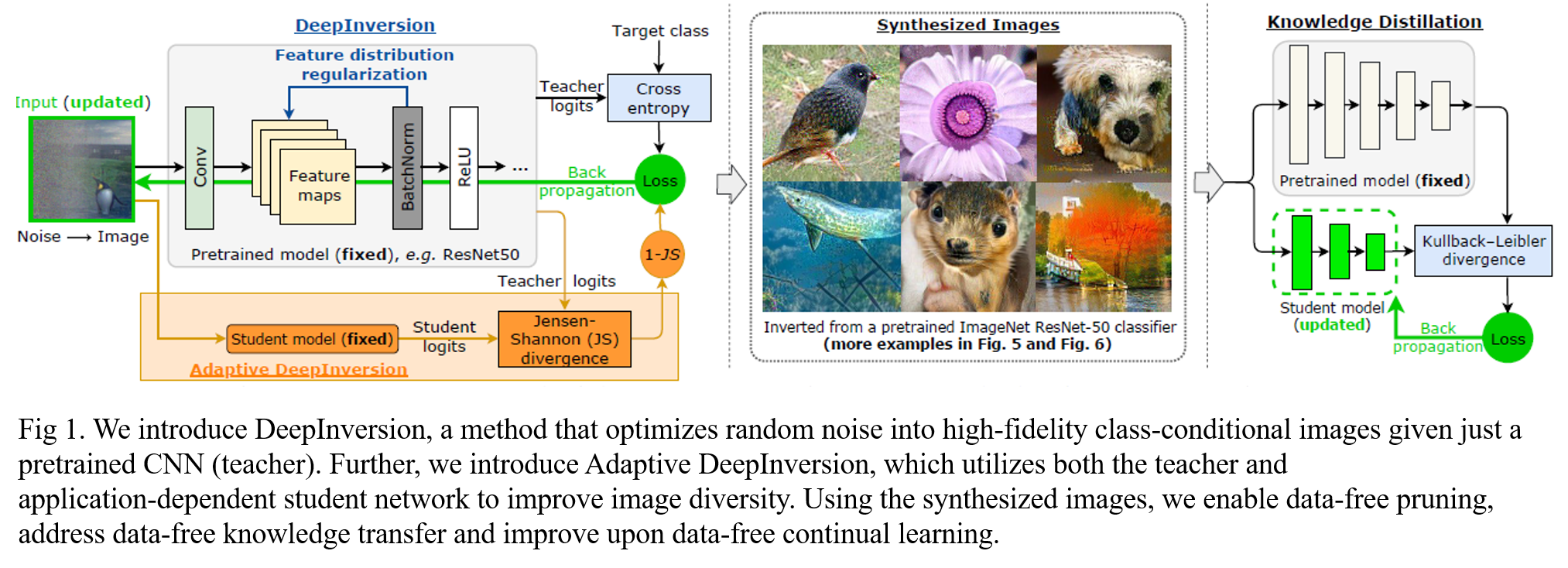
The overall procedure of our method is described in Fig. 1.
2.1 Background
2.1.1 Knowledge distillation
Given a trained model \(p_T\) and a dataset \( \mathcal{X} \), the parameters of the student model, \( W_S\), can be learned by
\[
min_{, W_S} \sum_{ x \in \mathcal{X} } KL( p_T(x), p_S(x) ), \quad \cdots Eq. (1)
\]
where \(KL( \cdot )\) refers to the Kullback-Leibler divergence and \( p_T(x)= p(x, W_T) \) and \( p_S(x)=p(x, W_S) \) are the output distributions produced by the teacher and student model, respectively, typically obtained using a high temperature on the softmax.
2.1.2 DeepDream
DeepDream synthesize a large set of images \( \widehat{x} \in \widehat{\mathcal{X}} \) from noise that could replace \(x \in \mathcal{X}\).
Given a randomly initialized input \( \widehat{x} \in \mathcal{R}^{H \times W \times C} \) and an arbitrary target label \( y \), the image is synthesized by optimizing
\[
min_{\widehat{x}} L(\widehat{x},y) + \mathcal{R} ( \widehat{x} ), \quad \cdots Eq. (2)
\]
where \(L(\cdot) \) is a classification loss (e.g. cross-entropy), and \( \mathcal{R} ( \cdot ) \) is an image reularization term, which steers \( \widehat{x} \) away from unrealistic images wit no discernible visual information:
\[
\mathcal{R}_p ( \widehat{x} ) = \alpha_T \mathcal{R}_T (\widehat{x}) + \alpha_L \mathcal{R}_L (\widehat{x}), \quad \cdots Eq. (3)
\]
where \(\mathcal{R}_T \) and \( \mathcal{R}_L \) penalize the total variance and \(l_2 \) norm of \(\widehat{x} \).
2.2 DeepInversion (DI)
We improve DeepDream's image quality by extending image regularization \( \mathcal{R} (\widehat{x}) \) with a new feature distribution regularization term.
To effectively enforce feature similarities between \(x \) and \( \widehat{x} \) at all levels (layers), we propose to minimize the distance between feature map statistics for \( x \) and \( \widehat{x} \). We assume that feature statistics follow the Gaussian distribution across batches and then can be defined by mean \( \mu \) and variance \( \sigma^2 \). Therefore, the feature distribution regularization term can be formulated as:
\[
\mathcal{R}_{feature} (\widehat{x}) = \sum_l \Vert \mu_l (\widehat{x}) - \mathbb{E}(\mu_l (x) \| \mathcal{X}) \Vert_2 +\sum_l \Vert \sigma_l (\widehat{x}) - \mathbb{E}(\sigma_l (x) \| \mathcal{X}) \Vert_2, \quad \cdots Eq. (4)
\]
where \( \mu_l (\widehat{x}) \) and \( \sigma^2_l (\widehat{x}) \) are the batch-wise mean and variance estimates of feature maps corresponding to the \( l \)-th convolutional layer. Obtaining \( \mathbb{E} ( \mu_l (x) | \mathcal{X} ) \) and \( \mathbb{E} ( \sigma^2_l (x) | \mathcal{X} )\) is that we extract running average statistics stored in the widely-used BatchNorm (BN) layers. It implicitly captures the channel-wise means and variances during training, hence allows for estimation of the expectations in Eq. (4) by:
\[
\begin{array}{l} \mathbb{E} (\mu_l (x) \| \mathcal{X}) \simeq BN_l (running\_mean), \quad \cdots Eq. (5) \cr \mathbb{E} (\sigma^2_l (x) \| \mathcal{X}) \simeq BN_l (running\_variance). \quad \cdots Eq. (6) \end{array}
\]
We refer to this model inversion method as DeepInversion. \( R(\cdot) \) can thus be expressed as
\[
\mathcal{R}_D (\widehat{x}) = \mathcal{R}_p ( \widehat{x}) +\alpha_f \mathcal{R}_F (\widehat{x}). \quad \cdots Eq. (7)
\]
2.3 Adaptive DeepInversion (ADI)
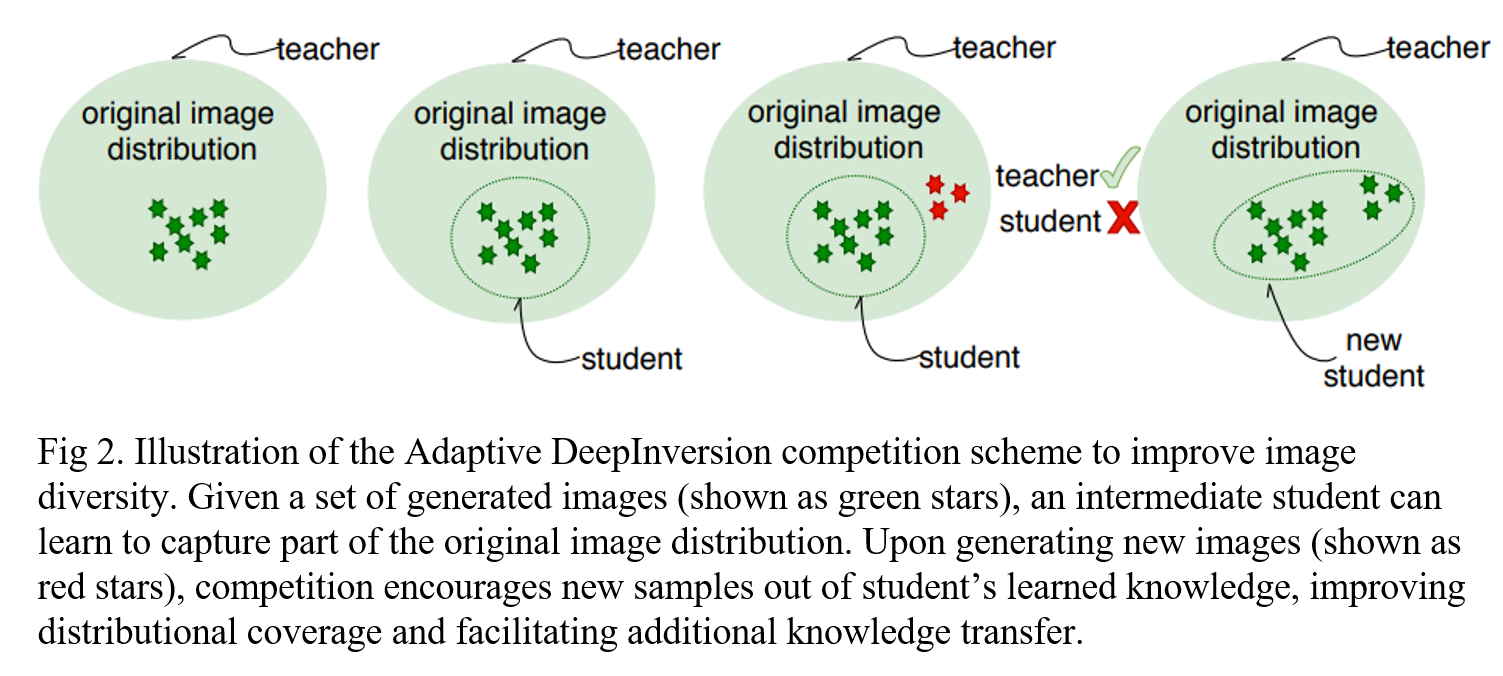
Diversity also plays a crucial role in avoiding repeated and redundant synthetic images. For this, we propose Adaptive DeepInversion, an enhanced image generation scheme based on an iterative competition scheme between the image generation process and the student network. The main idea is to encourage the synthesized images to cause student-teacher disagreement.
Then, we introduce an additional loss \( \mathcal{R}_{c} \) for image generation based on the Jensen-Shannon divergence that penalizes output distribution similarities,
\[
\begin{array}{l} \mathcal{R}_{c} (\widehat{x}) = 1- JS(p_T(\widehat{x}), p_S (\widehat{x})), \cr JS(p_T(\widehat{x}), p_S (\widehat{x}))= \frac{1}{2} ( KL (p_T (\widehat{x}),M)+KL (p_S (\widehat{x}),M)), \end{array} \quad \cdots Eq. (8)
\]
where \( M=\frac{1}{2} \cdot ( p_T (\widehat{x} )+p_S (\widehat{x})) \) is the average of the teacher and student distributions.
During optimization, this new term leads to new images the student cannot easily classify whereas the teacher can. As illustrated in Fig 2. our proposal iteratively expands the distributional coverage of the image distribution during the learning process. The regularization \( \mathcal{R} ( \cdot ) \) from Eq.(7) is updated with an additional loss scaled by \( \alpha_c \) as
\[
\mathcal{R}_A (\widehat{x})= \mathcal{R}_D(\widehat{x}) +\alpha_c \mathcal{R}_c(\widehat{x}) \quad \cdots Eq. (9)
\]
Reference
Yin, Hongxu, et al. "Dreaming to distill: Data-free knowledge transfer via DeepInversion." Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2020.
Github Code: Dreaming to Distill
'AI paper review > Model Compression' 카테고리의 다른 글
| EagleEye: Fast Sub-net Evaluation for Efficient Neural Network Pruning (0) | 2022.03.10 |
|---|---|
| Data-Free Knowledge Amalgamation via Group-Stack Dual-GAN (0) | 2022.03.09 |
| Zero-Shot Knowledge Transfer via Adversarial Belief Matching (0) | 2022.03.08 |
| Data-Free Learning of Student Networks (0) | 2022.03.08 |
| Zero-Shot Knowledge Distillation in Deep Networks (0) | 2022.03.08 |
