1. What is data-free knowledge distillation??
Knowledge distillation: Dealing with the problem of training a smaller model (Student) from a high capacity source model (Teacher) so as to retain most of its performance.
As the word itself, We perform knowledge distillation when there is no original dataset on which the Teacher network has been trained. It is because, in real-world, most datasets are proprietary and not shared publicly due to privacy or confidentiality concerns.
In order to perform data-free knowledge distillation, it is necessary to reconstruct a dataset for training Student network. Then, in this paper, we propose "Zero-Shot Knowledge Distillation" (ZSKD), which performs pseudo data synthesis from the Teacher model that acts as the transfer set to perform the distillation without even using any meta-data.

2. Method
2.1 Knowledge Distillation
Transferring the generalization ability of a large, complex Teacher \( T \) deep neural network to a less complex Student (\(S\)) network can be achieved using the class probabilities produced by a Teacher as "soft targets" for training the Student.
Let \( T\) be the Teacher network with learned parameters \( \theta_T \)and \( S \) be the Student with parameters $\theta_S$, note that in general \( \vert \theta_S \vert \ll \vert \theta_T \vert \).
Knowledge distillation methods train the Student by minimizing the following objective ((L)).
\[
L=\sum_{(x,y) \in \mathbb{D}} L_K (S(x,\theta_S,\tau), T(x,\theta_T, \tau))+\lambda L_C( \widehat{y}_S,y)
\]
,where \(D\) is training dataset, \(L_C\) is the cross-entropy loss computed on the labels \( \widehat{y}_S \) predicted by the Student and ground truth \(y\). \(L_K\) is the distillation loss (e.g. cross-entropy or MSE), \( (T(x,\theta_T,\tau)\) indicates the softmax output of the Teacher and \(S(x,\theta_S, \tau)\) denotes the softmax output of the Student. Note that, unless it is mentioned, we use a temperature (\(\tau\)) of 1.
2.2 Modelling the Data in Softmax Space
In Zero-Shot Knowledge Distillation in Deep Networks, we deal with the scenario where we have no access to (i) any training data samples (either from the target distribution or different) (ii) meta-data extracted from it.
To tackle this, our approach taps the learned parameters of the Teacher and produces synthesized input representations, named Data Impressions (DIs), from the underlying data distribution on which it is trained. These can be used as a transfer set in order to perform knowledge distillation to a Student model.
In order to craft the Data impressions, we model the output space of the Teacher model. Let \( s \sim p(s)\), be the random vector that represents the softmax outputs of the Teacher, \(T(x, \theta_T)\). We model \(p(s^k)\) belonging to each class \(k\), using Dirichlet distribution.
Dirichlet distribution: \(Dir(x_1, \cdots x_K, \alpha_1, \cdots, \alpha_K) ; s.t. ; \sum^K_i x_i =1 ;and; x_i \geq 0 ; \forall i\)
The distribution to represent the softmax output \(s^k\) of class \(k\) would be modelled as, \(Dir(K,\alpha^k)\) where \(k \in {1 \cdots K}\) is the class index, \(K\) is the dimension of the output probability vector and \(\alpha^k\) is the concentration parameter of the distribution modelling class \(k\), where \(\alpha^k=[\alpha^k_1, \cdots \alpha^k_K]\) and \(\alpha^k_i>0, \forall i \).
2.2.1 Concentration Parameter (\(\alpha\))
Concentration parameter \(\alpha\) can be thought of as determining how "concentrated" the probability mass of a sample from a Dirichlet distribution is likely to be.
| If \(\alpha \ll 1 \) \(\rightarrow\) the mass is highly concentrated in only a few components|
| Elif \(\alpha \gg 1 \) \(\rightarrow\) the mass is dispersed almost equally among all the components|
So, it is important to determine right \(\alpha\). We make its values to reflect the similarities across the components in the softmax vector. Since these components denote the underlying categories in the recognition problem, \(\alpha\) should reflect the visual similarities among them.
Thus, we resort to the Teacher network for extracting this information. We compute a normalized class similarity matrix (\(C\)) using the weights \(W\) connecting the final (softmax) and the pre-final layers. The element \(C(i,j)\)of this matrix denotes the visual similarity between the categories \(i\) and \(j\) in [0,1].

2.2.2 Class Similarity Matrix (\(C\))
The weights \(w_k\) can be considered as the template of the class \(k\) learned by the Teacher network. This is because the predicted class probability is proportional to the alignment of the pre-final layer’s output with the template \(w_k\).
|If pre-final layer's output is positive scaled version of \(w_k\) \(\rightarrow\) predicted probability for class \(k\) peaks|
|Elif pre-final layer's output is misaligned with the \(w_k\) \(\rightarrow\) predicted probability for class \(k\) is reduced|
Therefore, we treat the weights \(w_k\) as the class template for class \(k\) and compute the similarity between classes \(i\) and \(j\) as:
\[
C(i,j)=\frac{w^T_i w_j}{\Vert w_i \Vert \Vert w_j \Vert}.
\]
Since the elements of the concentration parameter have to be positive real numbers, we perform a min-max normalization over each row of the class similarity matrix.
2.3 Crafting Data Impression via Dirichlet Sampling
Once the parameters \(K\) and \(\alpha^k\) of the Dirichlet distribution are obtained for each class \(k\), we can sample class probability (softmax) vectors. As we optimize the following equation, we obtain the input representations (Data Impressions).
\[
\overline{x}^k_i=argmin_x L_C(y^k_i, T(x, \theta_T, \tau))
\]
\(Y^k=[ y^k_1,y^k_2, \cdots ,y^k_N ] \in \mathbb{R}^{K \times N}\) is the \(N\) softmax vectors corresponding to class \(k\), sampled from \(Dir(K,\alpha^k)\) distribution. Corresponding to each sampled softmax vector \(y^k_i\), we can craft a Data Impression \(\overline{x}^k_i\), for which the Teacher predicts a similar softmax
We initialize \(\overline{x}^k_i\) as a random noisy image and update it over multiple iterations till the cross-entropy loss between the sampled softmax vector \(y^k_i\) and the softmax output predicted by the Teacher is minimized. And the process is repeated for each of the \(N\) sampled softmax probability vectors in \(Y^k\), \(y \in {1, \cdots, K}\)
2.3.1 Scaling Factor (\(\beta\))
The probability density function of the Dirichlet distribution for \(K\) random variables is a \(K-1\) dimensional probability simplex that exists on a \(K\) dimensional space. Since we treat Dirichlet distribution, it is important to discuss the significance of the range of \(\alpha_i \in \alpha\), in controlling the density of the distribution.
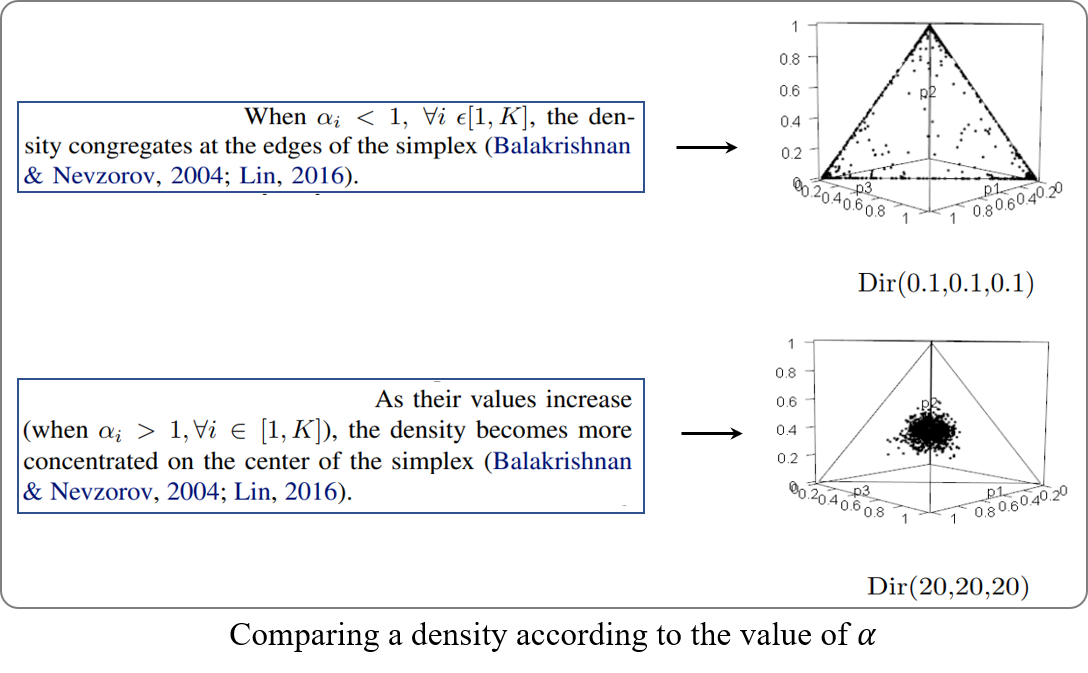
Thus, we define a scaling vector \(\beta\) which can control the range of the individual elements of the concentration parameter, which in turn decides regions in the simplex from which sampling is performed. This becomes a hyper-parameter for the algorithm. Thus, the actual sampling of the probability vectors happen from \(p(s)=Dir(K,\beta \times \alpha)\).
|If small value of \(\beta\) \(\rightarrow\) Variance of the sampled simplexes is high|
|Elif large value of \(\beta\) \(\rightarrow\) Variance of the sampled simplexes is low|
2.4 Zero-Shot Knowledge Distillation
We treat Data Impressions as the 'Transfer set' and perform knowledge distillation as follows.
\[
\theta_S=argmin_{\theta_S} \sum_\overline{x} L_K (S(\overline{x},\theta_S,\tau), T(\overline{x},\theta_T, \tau))
\]
We ignore the cross-entropy loss \(L_C\) from the general Distillation objective function. The proposed ZSKD approach is detailed in Algorithm 1.

3. Experiment Setting & Result

Reference
Nayak, Gaurav Kumar, et al. "Zero-Shot Knowledge Distillation in Deep Networks." International Conference on Machine Learning. 2019.
Github Code: Zero-Shot Knowledge Distillation in Deep Networks
'AI paper review > Model Compression' 카테고리의 다른 글
| EagleEye: Fast Sub-net Evaluation for Efficient Neural Network Pruning (0) | 2022.03.10 |
|---|---|
| Data-Free Knowledge Amalgamation via Group-Stack Dual-GAN (0) | 2022.03.09 |
| Dreaming to Distill Data-free Knowledge Transfer via DeepInversion (0) | 2022.03.09 |
| Zero-Shot Knowledge Transfer via Adversarial Belief Matching (0) | 2022.03.08 |
| Data-Free Learning of Student Networks (0) | 2022.03.08 |
