1. Introduction
Knowledge distillation: Dealing with the problem of training a smaller model (Student) from a high capacity source model (Teacher) so as to retain most of its performance.

1.1 Motivation
The compression methods such as pruning and filter decomposition require fine-tuning to recover performance. However, fine-tuning suffers from the requirement of a large training set and the time-consuming training procedure.
1.2 Goal
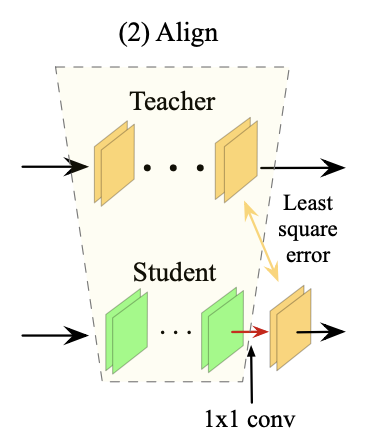
For realizing both data efficiency and training efficiency, this paper proposes a novel method, namely few-sample knowledge distillation (FSKD) with none of labels. The authors of this paper treat the original network as teacher-net and the compressed network as student-net. A 1x1 convolution layer is added at the end of each layer block of the student-net and then aligns the block-level outputs of the student-net with the teacher-net by estimating the parameters of the added layer.
2. Method
2.1 Overview

FSKD method consists of three steps:
- Obtaining a student net either by pruning or by decomposing the teacher net.
- Adding a 1x1 conv-layer at the end of each block of student-net and align the block-level outputs between teacher and student by estimating the parameters of the added layer.
- Merging the added 1x1 conv-layer into the previous conv-layer so that extra parameters and computation cost is not required on the student-net.
Three reasons make the idea works efficiently.
- Adding 1x1 conv-layer is enough to calibrate student-net and recover performance.
- The 1x1 conv-layers have relatively fewer parameters.
- The block-level output from teacher-net provides rich information as shown in FitNet.
2.2 Block-level Alignment
- \( X^s , X^t \): the block-level output in matrix form for the student and teacher, respectively.
- \( X^s , X^t \in \mathcal{R}^{n_o \times d }\): supposing both network's output sizes are same.
- \( d \): the per-channel feature map resolution size.
- \( n_o \): the number of output channels
- \( X^s , X^t \in \mathcal{R}^{n_o \times d }\): supposing both network's output sizes are same.
- \( Q \): 1x1 conv-layer
They add a 1x1 conv-layer \( Q \) at the end of each block of student-net before non-linear activation.
As \( Q \) is degraded to the matrix form, it can be estimated with least squared regression as:
\[
Q^* = argmin_Q \sum^N_i \lVert Q * X^s_i - X^t_i \rVert , \quad \cdots (1)
\]
where \( N \) is the number of label-free samples used, and \( *\) means matrix product. The number of parameters of \( Q \) is \( n_o \times n_o \).
Suppose there are \( M \) corresponding blocks in the teacher and student required to align. To achieve our goal, minimize the following loss function
\[
L(Q_j) = \sum^M_j \sum^N_i \lVert Q * X^s_{ij} - X^t_{ij} \rVert_F , \quad \cdots (2)
\]
where \( Q_j \) is the tensor for the added 1x1 conv-layer of the \(j\)-th block.
In practice, the authors optimize this loss with a block coordinate descent (BCD) algorithm, which greedily handles each of the \(M\) blocks in the student sequentially. They also use FSKD with standard SGD but, they experimentally showed that FSKD with BCD is more efficient: (1) Each \( Q \) can be solved with the same set of few samples by aligning the block-level outputs between student and teacher. (2) The BCD can be done in less than a minute.
2.3 Mergeable 1x1 conv-layer
In this section, They prove that the added 1x1 conv-layer can be merged into the previous conv-layer without introducing additional parameters and computation cost.
Theorem 1
A pointwise convolution with tensor \( Q \in \mathcal{R}^{n'_o \times n'_i \times 1 \times 1 }\) can be merged into the previous convolution layer with tensor \( W' \in \mathcal{R}^{ n_o \times n_i \times k \times k } \) to obtain the merged tensor \( W' = Q \circ W \), where \( \circ \) is merging operator and \( W' \in \mathcal{R}^{ n'_o \times n_i \times k \times k } \) if the following conditions are satisfied.
c1. The output channel number of \( W \) equals to the input channel number of \( Q \), i.e., \( n_o=n'_i\) .
c2. No non-linear activation layer like ReLu between \( W\) and \( Q \).
The pointwise convolution can be viewed as a linear combination of the kernels in the previous convolution layer. This implies that the two layers are integrated into one layer. However, the number of output channels of \( W' \) is \( n'_o \), which is different from that of \( W \). It is easy to have the following corollary.
Corollary 1. When the following condition is satisfied,
c3. the number of input and output channels of * \( Q\) *equals to the number of output channel of \( W \), i.e., \( n'_i = n'_o = n_o \), \( Q \in \mathcal{R}^{ n_o \times n_o \times 1 \times 1 } \), the merged convolution tensor \( W' \) has the same parameters and computation cost as \( W \) , i.e. both \( W', W \in \mathcal{R}^{n_o \times n_i \times k \times k }\).
This condition is required not only for ensuring the same parameter size and computing cost, but also for ensuring the output size of the current layer matching to the input of next layer.
The overall algorithm of FSKD is described in the below figure.

3. Experiment Setting
For all experiments, the results are averaged over 5 trials of different randomly selected images. Considering the number of channels in teacher may be different from that in student, they only match the un-pruned part of feature maps in teacher-net to the feature maps in the student net as shown in Fig 2. And, Fig 3 represents how FSKD works for block-level alignment.

4. Experiment Result


Reference
Li, Tianhong, et al. "Few sample knowledge distillation for efficient network compression." Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2020.
'AI paper review > Model Compression' 카테고리의 다른 글
| Learning Features with Parameter-free Layers 논문 리뷰 (0) | 2022.04.28 |
|---|---|
| Learning Low-Rank Approximation for CNNs (0) | 2022.03.12 |
| Knowledge Distillation via Softmax Regression Representation Learning (0) | 2022.03.10 |
| EagleEye: Fast Sub-net Evaluation for Efficient Neural Network Pruning (0) | 2022.03.10 |
| Data-Free Knowledge Amalgamation via Group-Stack Dual-GAN (0) | 2022.03.09 |